Горное небо - для вас!

Часть первая.

Позволим себе вольный полет технической фантазии в жестких рамках законов физики и геометрии. Рассуждать мы будем на тему общих взаимосвязей между различными параметрами конструкции ракеты, запускаемой с Земли в космос. Итак, начнем.
Примем форму ракеты как конус. Хотя её в той же мере можно принять и как пирамиду, так как это не повлияет на ход дальнейших рассуждений, ибо формула для нахождения объема этих тел одинакова: одна треть площади основания помноженного на высоту:

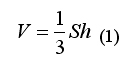
где  V - это объем тела,  S - площадь основания, h – высота тела.

Масса тела будет вычисляться по формуле:

где M - это масса тела, ρ – кажущаяся плотность тела, V – объем тела.
Введем особый параметр, характеризующий конструкцию ракеты, который в ракетной технике не используется. Речь идет о поверхностной плотности тяги. Смысл этого параметра: так как в данной конструкции ракеты используется определенный тип двигателей, которые дают некоторую тягу и при этом занимают определенное место на днище ракеты, то на всем днище ракеты можно разместить только определенное количество двигателей, с учетом технологически необходимых промежутков между ними. Таким образом, на единицу площади днища будет приходиться какое-то определенное количество тяги двигателей. Это и есть поверхностная плотность тяги, а именно тяга всех двигателей, отнесенная к площади днища (основания) ракеты. В виде математических символов это будет выглядеть так:

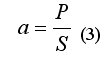
где a – это поверхностная плотность тяги, P – суммарная тяга двигателей, S – площадь днища ракеты (основания).
Введем еще один параметр – коэффициент избытка тяги. Смысл этого коэффициента: двигатели ракеты на старте дают некоторое количество тяги, если эта тяга будет меньше или равна весу ракеты, то ракета никуда не полетит; отрыв ракеты от стартового стола и полет возможны, только если тяга двигателей будет больше веса ракеты. Должен иметься избыток тяги против веса ракеты, который будет выражаться как отношение тяги двигателей к весу ракеты. Пойдем ради упрощения на ухищрение, принятое в технике – будем выражать вес (силу) и тягу двигателей не ньютонах, а в тоннах или килограммах силы. Тогда мы можем принять вес равный массе и спокойно делить на него тягу двигателей:

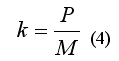
где k – это коэффициент избытка тяги, P – суммарная тяга двигателей, M – масса ракеты.

Теперь у нас есть все необходимые для дальнейших преобразований формулы. Начинаем собирать всё в кучу.
Из формулы (4) выразим массу ракеты М:

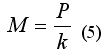
Из формулы (3) выразим тягу двигателей P:

Подставим значение P из формулы (6) в формулу (5). Получаем:

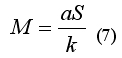
Теперь из формулы (2) выразим объем тела V:

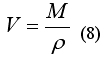
Подставим полученное значение V в формулу (1):

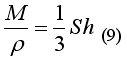
Выразим из формулы (9) массу ракеты M:

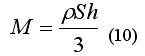
Теперь подставим значение массы ракеты М из формулы (10) в формулу  (7):
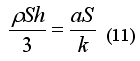из которой получаем:  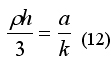 и далее выражаем отсюда высоту ракеты h:

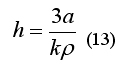
Из полученной формулы (13) можно заключить, что при данных технических условиях, которые фиксируют (превращают в константы) значения поверхностной плотности тяги a, коэффициента избытка тяги k и кажущейся плотности ρ, и само значение высоты ракеты тоже превращается в константу. Увеличить высоту ракеты можно только уменьшив избыток тяги и/или уменьшив кажущуюся плотность, либо увеличив поверхностную плотность тяги. Тек как в реальности желателен больший избыток тяги и большая кажущаяся плотность ракеты (боле плотные компоненты топлива, более рациональная и плотная компоновка узлов ракеты), то сознательное уменьшение этих параметров вряд ли возможно и рационально. А вот увеличение плотности тяги на днище ракеты это самый реальный путь получить возможность увеличить высоту ракеты. Это если стремиться увеличить грузоподъемность ракеты, сохраняя неизменной площадь днища.
Но если мы реально уперлись в технически достижимый потолок по параметрам поверхностной плотности тяги, кажущейся плотности и избытку тяги, ведь возможности совершенствовать двигатели, уменьшать их габариты и увеличивать тягу, ограничены законами термодинамики и газовой динамики, плотность топлив тоже варьирует только в тех пределах, насколько позволяют химические свойства веществ. И если мы уже зажаты между этими условиями и достигли технически достижимых пределов в совершенствовании конструкции ракеты, но нам необходимо построить ракету гораздо большей грузоподъемности то единственный возможный конструктивный путь это увеличивать площадь основания. Это явно видно из формулы (13) – площадь основания S остается независимой переменной.

И вот теперь перейдем более наглядным примерам. Самые большие из построенных людьми ракет это Сатурн-5 в США и Н-1 в СССР. Обе ракеты предназначались для выполнения лунной программы, и в общем и целом сходны по своим параметрам. Масса ракет около 3000 тонн, высота колеблется около 100 метров, форма ракет приближается в форме стройного конуса (особенно это заметно у Н-1, так как там на всех ступенях использовалось одно и то же топливо – кислород+керосин, а вот у Сатурна-5 на второй и третьей ступенях использовались водород+кислород, что сказалось и на форме ракеты). Примем параметры этих ракет за исходные для наших теоретических ракет и близкие к техническому пределу, хотя наверно возможны еще улучшения параметров ракет, но не боле чем в 1,5-2 раза.
Таким образом, высота теоретической сверхтяжелой ракеты останавливается на отметке около 100-110 метров. Единственное место, которое мы можем изменять это днище ракеты, мы его можем расширять. По мере роста наших запросов к грузоподъемности ракеты будет расти не высота ракеты, а площадь основания, и ракета из стройного конуса будет превращаться во всё более широкий конус (или пирамиду). Чем шире она будет становиться, тем большее аэродинамическое сопротивление ракета будет испытывать при полете через атмосферу. В итоге законы аэродинамики остановят разрастание основания ракеты вширь, так как преодоление сопротивления воздуха будет съедать всю прибавку в суммарной тяге двигателей.

часть вторая